

Frontline Learning Research Vol.11 No. 1 (2023) 40 - 56
ISSN 2295-3159
aJohannes Gutenberg-University Mainz, Germany
b Stanford University, USA
Article received 8 June 2022/ revised 30 January 2023/ accepted 1 February 2023/ available online 22 March 2023
Quantitative reasoning is considered a crucial prerequisite for acquiring domain-specific expertise in higher education. To ascertain whether students are developing quantitative reasoning, validly assessing its development over the course of their studies is required. However, when measuring quantitative reasoning in an academic study program, it is often confounded with other skills. Following a situated approach, we focus on quantitative reasoning in the domain of business and economics and define domain-specific quantitative reasoning primarily as a skill and capacity that allows for reasoned thinking regarding numbers, arithmetic operations, graph analyses, and patterns in real-world business and economics tasks, leading to problem solving. As many studies demonstrate, well-established instruments for assessing business and economics knowledge like the Test of Understanding College Economics (TUCE) and the Examen General para el Egreso de la Licenciatura (EGEL) contain items that require domain-specific quantitative reasoning skills. In this study, we follow a new approach and assume that assessing business and economics knowledge offers the opportunity to extract domain-specific quantitative reasoning as the skill for handling quantitative data in domain-specific tasks. We present an approach where quantitative reasoning – embedded in existing measurements from TUCE and EGEL tasks – will be empirically extracted. Hereby, we reveal that items tapping domain-specific quantitative reasoning constitute an empirically separable factor within a Confirmatory Factor Analysis and that this factor (domain-specific quantitative reasoning) can be validly and reliably measured using existing knowledge assessments. This novel methodological approach, which is based on obtaining information on students’ quantitative reasoning skills using existing domain-specific tests, offers a practical alternative to broad test batteries for assessing students’ learning outcomes in higher education.
Keywords: quantitative reasoning; confirmatory factor analysis; domain-specific learning; higher education; business and economics.
Within many study domains, quantitative reasoning is a required skill for scientific reasoning and arguing. Furthermore, in study domains or subjects with a strong quantitative focus, quantitative reasoning is not only a required generic skill in terms of developing and understanding scientific arguments, but it is also necessary to understand domain-specific concepts, such as the supply-demand-function in economics or amortization plans in business. Though quantitative reasoning is not necessarily explicitly taught in higher education classes, it is nonetheless part of learning and applying quantitative operations within business and economics tasks.
While there are many studies and assessments that measure general quantitative reasoning (for an overview, Roohr et al., 2014), there is a lack of research addressing the development of quantitative reasoning in specific domains, including the domain of business and economics.
While business and economics outcome measures do not explicitly measure quantitative reasoning, they contain numerous items that demand reasoning quantitatively. The question, then, is: can quantitative reasoning be isolated from test items found on business and economics outcome measures? If it can, a separate measure of quantitative reasoning would not be necessary to track students’ development of quantitative reasoning.
Especially in the context of the so-called Bologna reform in Europe with its increasing modularization, the number of examinations and assessments in higher education has increased significantly. Therefore, the research question arises as to what information on students’ quantitative reasoning ability can be obtained using the existing domain-specific tests to avoid the practically less suitable use of broad test batteries in higher education. To this end, we introduce a novel approach by isolating an assessment to measure quantitative reasoning from existing tests instead of developing a new test for this purpose. Using confirmatory factor analysis (CFA), we show that a combination of questions from existing business and economics assessments provide a valid and reliable measure of quantitative reasoning.
In the domain of business and economics, there are several validated and internationally established tests used to assess knowledge-related competences. For instance, there are the Test of Understanding College Economics (TUCE) (Walstad et al., 2007) and the Examen General para el Egreso de la Licenciatura (EGEL) (CENEVAL, 2011), which are standardized instruments adapted and validated in different language versions so that they can be used for assessing higher education students in different countries. The TUCE, originally developed in the US, has been adapted and validated for German, Japanese, Korean and many more languages and higher education contexts (Walstad et al., 2007; Yamaoka et al., 2010). For Germany, there is also a valid adaption of EGEL that has been used to assess knowledge in business administration (Zlatkin-Troitschanskaia et al., 2014).
Since these instruments are validated for measuring knowledge in business and economics, it is unclear whether they can also provide a reliable and valid tool for the assessment of quantitative reasoning as one sub-facet of overall business and economics competence within this domain. To define the assessment design for quantitative reasoning out of the existing business and economics tests, we follow Mislevy & Haertel’s (2006) evidence-centered design and focus on the following three steps:
The aim of this study, then, is to explore if we can isolate, conceptually, quantitative reasoning items on the TUCE and EGEL and bring item-response data to bear on the claim that the subset of items actually measure quantitative reasoning.
In the following, we briefly review current conceptual and empirical research on quantitative reasoning and its measurement (Section 2). In Section 3, we develop four hypotheses related to the overarching research question driving this study—whether a subset of the EGEL and TUCE items can be used to reliably and validly assess the underlying and implicitly measured construct of quantitative reasoning in business and economics (in accordance with AERA et al., 2014). In Sections 4 and 5, we conduct conceptual and empirical analyses of the items to explore the claim that a subset of them measures quantitative reasoning. We conclude that we can empirically identify a reliable and valid subset of items that conceptually measure quantitative reasoning (and verbal reasoning) in existing business and economics knowledge tests (Section 6).
There is a growing consensus that effective learning and citizenship in the 21st century requires college graduates to be ‘quantitatively literate’, that is, to be able to think and reason quantitatively when the situation demands it (Shavelson, 2008; Ball, 2003; Madison, 2009; NRC, 2012). Universities are beginning to recognize the need for such quantitative competencies and consider them essential student learning outcomes (SLOs) (Lusardi & Wallace, 2013). For instance, in a study among the member institutions of the American Association of Colleges and Universities (AAC&U), 71% of the colleges and universities identified the acquisition of quantitative reasoning as a central aim of learning in higher education (Hart Research Associates, 2009). Similarly, the National Leadership Council for Liberal Education and America’s Promise (LEAP) named quantitative reasoning as one of the essential SLOs of the new global century (AAC&U, 2008). quantitative reasoning is a component of tertiary education as it is one of four key SLOs (the others being: writing, critical thinking, and information and technological literacy) (Davidson & McKinney, 2001).
Quantitative reasoning is considered more than the ability to perform rough calculations. It is an essential competence and crucial prerequisite for acquiring domain-specific and generic knowledge and skills in higher education. In comparison to mathematics as a particular discipline, quantitative reasoning can be considered a generic skill and a way of thinking that requires dealing with complex, real-world, everyday challenges involving quantities and their different kinds of representations in different disciplines (Davidson & McKinney, 2001).
Following a situated theoretical approach (Shavelson, 2008), we assume that this generic skill can be manifested differently in varying domain-specific contexts. In this study, we focus on quantitative reasoning in the domain of business & economics (B&E) and define domain-specific quantitative reasoning (DSQR) primarily as a skill and capacity that allows for reasoned thinking regarding numbers, arithmetic operations, graph analyses, and patterns in real-world business and economics tasks, leading to problem-solving.
Quantitative reasoning is embedded in the hierarchical construct of cognitive outcomes. The hierarchical nature has five levels, which represent skills with a higher domain-specificity on lower levels and more generic skills on higher levels (Shavelson & Huang, 2003; Figure 1).

Figure 1. Framework for Cognitive Outcomes (Shavelson & Huang, 2003, p. 14).
A number of instruments have been used to assess quantitative reasoning as a generic skill such as the Quantitative Reasoning for College Science (QuaRCS) Test (Follette et al., 2017), the CLA+ with the Scientific and Quantitative Reasoning Test (SQR) (Zahner, 2013), the quantitative reasoning questions from the. Graduate Record Examination (GRE) and the HEIghten quantitative reasoning test (ETS, 2016) (for an overview, Roohr et al., 2014). Currently, however, teaching in higher education does not focus on developing quantitative reasoning in an explicit way, or on assessing it (Rocconi et al., 2013). This might be the reason why tests for quantitative reasoning are rarely used in higher education research and practice.
Rather the focus is more on the assessment of domain-specific competences. This said, domain-specific quantitative reasoning is seldom assessed although claimed to be an important outcome of a program of study. As if to do so requires a separate test from what is usually used, quantitative reasoning is unlikely to be assessed. However, the separate assessment of quantitative reasoning might not be necessary to measure the level and development of quantitative reasoning throughout undergraduate or graduate studies. If domain-specific knowledge tests can also provide a source for reliable and valid measurement of quantitative reasoning within a domain (O’Neill & Flynn, 2013), it could offer a practicable approach for higher education.
Students’ knowledge and skills are commonly assessed with domain-specific competence tests in various fields of study (physics, engineering, psychology, business and economics; for an overview of research on domain-specific competences in different domains, PIACC study OECD, 2013, or KoKoHs program, Zlatkin-Troitschanskaia et al., 2017). Following Elrod (2014), we suspect that quantitative reasoning is a component embedded in domain-specific tests. Therefore, separating quantitative reasoning loaded items within business and economics tests seems both reasonable and feasible. Furthermore, by measuring quantitative reasoning within domain-specific competence tests, teachers and students receive direct feedback on how quantitative reasoning contributes to solving domain-specific problems.
Indeed, in the domain of business and economics, we found no assessments of quantitative reasoning. The assessment of quantitative reasoning for indexing individual student skills or the effectiveness of curricula remains primarily a local practice (Gaze et al., 2014). Elrod (2014) assumes that one concern regarding quantitative reasoning assessment is the perception of quantitative reasoning as another outcome to assess aside from all the other regular tests and assessments and for which teachers or researchers may need to create a completely new assessment strategy. Therefore, providing a valid measure of quantitative reasoning to be assessed within a domain-specific knowledge test, would open up new opportunities for researchers and practitioners. Hereby, quantitative reasoning can be considered a ‘sub-dimension’ in existing assessment instruments.
In particular, the assessment of domain-specific business and economics knowledge and understanding offers the opportunity to extract quantitative reasoning as the skill to handle quantitative data and numbers in existing test items. When assessing knowledge in business and economics, the TUCE (Walstad et al., 2007) and EGEL (CENEVAL, 2011) contain items where quantitative reasoning skills are necessary, as Brückner and colleagues (2015b) demonstrate. Although these tests deal with standardized assessments with a multiple-choice (MC) format, students must complete items with domain-specific tasks with real-life economic questions or problems.
This study is based on an assessment of content knowledge in the domain of business and economics with items from the TUCE and EGEL (Section 4). We claim that items from the TUCE and EGEL can be classified based on whether quantitative reasoning or non-quantitative verbal reasoning was required to answer a question correctly (Brückner et al., 2015a for separating the TUCE items into quantitative reasoning and verbal reasoning). We define verbal reasoning as an ability that allows for reasoned thinking without numbers, arithmetic operations and patterns in business and economics tasks. Further, we can assume that spatial reasoning may link the two domains of quantitative reasoning and verbal reasoning. However, since there were very few tasks featuring graphs and diagrams in the two assessments considered here, it is not possible to model a third dimension with SR. Therefore, the assumption of whether SR presents an empirically separable construct from quantitative reasoning cannot be verified in this study.
By differentiating quantitative reasoning and verbal reasoning we assume that the way students deal with numerical or verbal content within a task influences the nature and difficulty of the solution. We suspected that some items would demand a preponderance of quantitative reasoning and some items verbal reasoning. By doing so, we focus on convergent and discriminant validity, including the quantitative reasoning’s relationship to other variables. Consequently, we analyzed multiple-choice items from the TUCE and EGEL to identify quantitative and verbal content demands. The sorting process is described in Section 4.
This study evaluates whether (1) it is possible to (a) identify subsets of items that conceptually measure quantitative reasoning in business and economicscontent knowledge tests, and (b) if this conceptual distinction can be empirically supported and distinguished from other achievement items of a verbal nature (verbal reasoning) (research question 1: internal construct validity). Further, (2) whether the resulting scores for quantitative reasoning provide valid measures regarding external criteria for the underlying construct (research question 2: convergent and discriminant validity).
We follow AERA et al.’s (2014) validation criteria, with particular focus on the criterion of internal structure—the extent to which the empirical structure of the test supports the conceptual structure. More specifically, we assume that quantitative reasoning and verbal reasoning subtext scores are highly correlated but empirically separable, each with high internal consistency (Hypothesis A).
In addition, if evidence supports a business and economics quantitative reasoning interpretation, we need to support this claim by showing that the quantitative reasoning score correlates, as expected, with a specific domain and with additional external variables.1 Only few such studies have been conducted and they show a relationship between quantitative reasoning and socio-demographic factors (Brückner et al., 2015b; Tiffin et al., 2014). In particular, male test takers have been found to perform better on numeracy tasks than female test takers (Owen, 2012; Williams et al., 1992). This finding indicates that gender effects might differ between assessments of different components of the business and economics achievement construct, that is, between quantitative reasoning and verbal reasoning (Yamaoka et al., 2010). In economics, higher levels of economics-related quantitative reasoning have been reported for male students, while higher levels of verbal reasoning have been reported for female students. In an introductory course in economics at a US university Ballard and Johnson (2004) found that male students had higher numeracy scores than female students. Moreover, Brückner et al. (2015a) found that both quantitative reasoning and verbal reasoning were higher for male than for female students. The same is evident in general for business and economics achievement scores: Male students generally perform better than female students (Brückner et al., 2015a; Happ et al., 2018). However, the gender-specific differences were larger, on average, for quantitative reasoning scores than for verbal reasoning scores. According to these findings, we expect male students to outperform female students on a business and economics quantitative reasoning subtest (Hypothesis B).
Moreover, migration background has been shown to impact generic skills, and quantitative reasoning in particular. In studies in Europe, students with a migration background score lower, on average, on tests in numerically oriented subdomains of business and economics such as economics (Zlatkin-Troitschanskaia et al., 2015), and finance (Förster et al., 2015). Similar results have been found in the U.S. regarding ethnicity and race. For instance, Bleske-Rechek and Browne (2014) have shown a gap between ethnic groups on both the GRE VR and quantitative reasoning average scores. Furthermore, white examinees’ verbal reasoning scores fall, on average, a full standard deviation above black minority examinees’ scores, and a half standard deviation higher than examinees from other underrepresented groups. Consequently, we expect students with a recent migration background, that is students with a least one parent not of German origin, have lower test results, on average, in tasks with quantitative reasoning demands than students without migration background (Hypothesis C).
The educational background prior to higher education also influences generic skills such as quantitative reasoning. In particular, the school leaving grade (GPA) is considered a valid indicator of a person’s general academic ability (Schuler et al., 1990) as well as a significant predictor of students’ academic performance in a domain. For instance, Kuncel and colleagues (2010) showed in their meta-analysis that graduates’ GPA positively correlates with their performance in quantitative reasoning tasks (r=0.23) and verbal reasoning tasks (r=0.29) on the GRE test. Findings based on tests that assess students’ content knowledge in subdomains of business and economics such as accounting (Byrne & Flood, 2008; Fritsch et al., 2015), finance (Förster et al., 2015), and macroeconomics (Zlatkin-Troitschanskaia et al., 2015) indicate that a correlation of this kind between the GPA and domain-specific test results also exists in the business and economics domain. Consequently, we expect there to be a positive relationship between school leaving grades (GPA) and tests that demand quantitative reasoning in business and economics (Hypothesis D).
Furthermore, students’ previous subject-related knowledge acquired through learning processes prior to university is highly important in the acquisition of domain-specific knowledge at university (Alexander & Jetton, 2003; Anderson, 2005; Happ et al., 2018). For the domain of business and economics, subject-related knowledge can be acquired in different ways prior to university. In Germany, many students acquire their higher education entrance qualification at vocational schools that offer advanced courses in business and economics indicating that students have prior content knowledge in business and economics when they enter university. Passing advanced courses in business and economics at vocational schools or completing commercial vocational training is associated with a higher level of content knowledge in business and economics subdomains (for economics, Brückner et al., 2015b; for accounting, Fritsch et al., 2015; for finance, Förster et al., 2015). However, this prior knowledge should only have a strong effect when acquiring (or predicting) domain-specific knowledge. As quantitative reasoning and verbal reasoning are generic skills, there should be little correlation between prior knowledge of business and economics and performance in these dimensions if the test is an appropriate measure for quantitative reasoning and verbal reasoning. It is assumed that students who have pursued advanced courses at vocational schools or who have completed commercial vocational training do not perform significantly better than students who do not have any prior education in business and economics in tasks that explicitly demand quantitative reasoning (Hypothesis E).
Students’ business and economics content knowledge and understanding were measured in the project WiwiKom2 (Zlatkin-Troitschanskaia et al., 2014). In this project, the TUCE and EGEL were adapted to the German language and higher education context and comprehensively validated (AERA et al., 2014; ITC, 2005).
The following analyses refer to the subtests in the areas of accounting and finance (16 items each from EGEL) and microeconomics (30 items from TUCE), where we use all test items from these areas. Each item consists of an item stem and four response options with one correct answer. Using our definitions of quantitative reasoning and verbal reasoning we sorted the 30 TUCE items and 32 EGEL items into these two categories (for quantitative reasoning and verbal reasoning example items from the microeconomics part, Figure 2). Based on the differentiation of whether a task contains numerical properties that can indicate students’ quantitative reasoning skills as described in Shavelson et al. (2019), the following analyses assume a dichotomous differentiation between items with numerical content (quantitative reasoning) and items without numerical content (verbal reasoning).

Figure 2. Two TUCE items from the dimension microeconomics (Walstad et al., 2007).
Following and expanding upon Brückner et al. (2015a), who already classified TUCE items into quantitative reasoning and verbal reasoning items, we noted whether numerical operations were contained in the case descriptions for both instruments, TUCE and EGEL. Items that contained numerical content and thus required students to apply mainly their mathematical abilities were classified as quantitative reasoning (for the microeconomics part of TUCE, following Brückner et al., 2015a), while items dealing with purely verbally described definitions, concepts or conceptual systems were classified as verbal reasoning (Table 1).
Table 1
Distribution of quantitative reasoning (QR) and verbal reasoning (VR) items from the three content-domains of the TUCE and EGEL
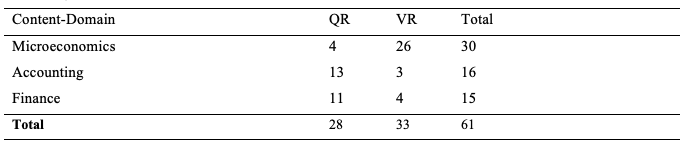
Like Brückner and colleagues (2015a), we achieved full congruence among the four different raters in the classification of the items into quantitative reasoning and verbal reasoning subsets in our study presented here (an interrater agreement of Cohens kappa=1.0; p=.000). Therefore, in response to research question 1a, we conclude that it is conceptually feasible to classify test items in a business and economics knowledge test into the categories quantitative reasoning and verbal reasoning. Based on this conclusion, we examined next whether the conceptual distinction between quantitative reasoning and verbal reasoning items can be empirically supported (RQ1b).
Data were collected in the summer semester 2015 using the abovementioned subtests from TUCE and EGEL. The test was administered as a paper-pencil test in a booklet design (Frey et al., 2009) using different sets of items from TUCE and EGEL within the booklets. The test booklets were randomly distributed among the participants.
The sample included 1,492 students from 27 universities and 13 universities of applied science throughout Germany. The institutions involved are a representative sample. At these universities, all beginning students enrolled in master’s degrees in business and economics were invited to participate in this study in the context of introductory courses that all beginning students in these degree courses have to attend; i.e., at each university, all students enrolled in a business and economics master’s degree were assessed at once in the context of a compulsory introductory lecture. The survey was carried out on site by trained test leaders. To encourage the students to participate in this study, every participant received €5 as well as individual feedback on the test results. Since participation was voluntary, the possibility of skewed representativeness at the student level cannot be excluded. However, the distribution of descriptive characteristics such as gender and age does not indicate any significant biases compared to overall student population in Germany. The composition of the sample in terms of the predictor variables we used is presented in Table 2.
Table 2
Distribution of the sample according to the predictors of domain-specific quantitative reasoning
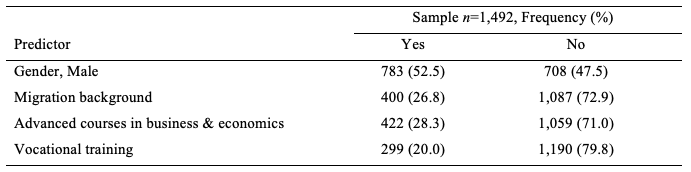
The two indicators – ‘attended an advanced course in business and economics at commercial upper secondary school’ and ‘completed vocational training’–were used as a proxy for prior knowledge in business and economics and operationalized as two dummy-coded variables in the following analysis (Section 5). The high school leaving grade (GPA) was used as an indicator of students’ general academic performance (mean=2.241, s.d=0.081 on a 5-point scale with 1 being the highest performance and 5 the lowest).
This study evaluates whether (1) it is possible to (a) identify subsets of items that conceptually measure quantitative reasoning in business and economics content knowledge tests, and (b) if this conceptual distinction can be empirically supported and distinguished from other achievement items of a verbal nature (verbal reasoning). Further, (2) whether the resulting scores for quantitative reasoning provide valid measures regarding external criteria for the underlying construct (research question 2: convergent and discriminant validity). As RQ 1a was answered to the affirmative above, attention now turns to questions 1b and 2 and the corresponding hypotheses.
We address this hypothesis by testing the fit of data to alternative models using confirmatory factor analysis (CFA) with the statistical package, Mplus 7.3 (Muthén & Muthén, 2012). All requirements for the structural equation model’s calculation were determined and were confirmed (Bagozzi & Yi, 1988). Model-1 posits two factors corresponding to quantitative reasoning and verbal reasoning. Model-2 posits a general reasoning factor combining quantitative reasoning and verbal reasoning.
We used a Maximum Likelihood estimator with robust standard errors (labeled MLR in Mplus) to take into account that item responses were dichotomous (0,1). Due to the combination of booklet design and dichotomous items, the selection was limited to maximum likelihood estimators. In Mplus, usually a weighted least squares estimator (WLSMV) is used for categorical variables. Furthermore, as the booklet design inevitably causes missing data patterns that must be taken into account, the modelling options are limited to CFA using Mplus’ options. We chose the MLR estimator, as this estimator enabled us to conduct a robust chi-square difference test. To examine the difference between the two CFA models, the 𝜒² difference test was performed. If the 𝜒² value is significant, the more restrictive model fits the data significantly worse than the general model (Bagozzi & Yi, 1988). The results are presented in Table 3.
Table 3
Model fit of the calculated CFA models

Overall, both models showed a good fit to the data. The disattenuated correlation between quantitative reasoning and verbal reasoning in model Model-1 was 0.76 (p=.000) suggesting that while high, quantitative reasoning and verbal reasoning could be interpreted separately. To decide which model fit the data better, we calculated a 𝜒² difference test for the empirical comparison of both models, including the models’ correction factors in the comparison test formula. As a calculation of the difference test with MPlus 7.3 was not possible due to the applied ‘maximum likelihood’ estimator, we had to manually calculate the value. To this end, we applied the Satorra-Bentler scaled chi-square test statistic (Satorra & Bentler, 2010). For this purpose, the one-factor Model-2 is defined as the constrained model, the two-factor model-1 is defined as the freely estimated model, and the 𝜒² test of the difference of the 𝜒² values of the model (column 2 in Table 3) is used to conclude whether the reduction of the 𝜒² value in the freely estimated model is significant and whether it fits the data better than the constrained model. Conducting the 𝜒² difference test for the MLR estimated models resulted in a scaled 𝜒² value of the differences of 280.5 with one degree of freedom (df=1). Considering the 𝜒² statistic and its distribution, the 𝜒² difference test showed a p-value of 0.000 (Δ𝝌𝟐=280.5; Δ𝑑𝑓=1). Model-1 therefore had a significantly better fit than Model-2. AIC and BIC values can be used as additional indicators in model comparisons. A smaller value signifies a better data fit (Schreiber et al., 2006). The model comparison shows that Model-1 has lower AIC and BIC values and is therefore preferable to Model-2.
Thus, we were able to isolate a quantitative reasoning score consistent with Brückner et al. (2015a). Moreover, the reliabilities for the General Reasoning (one factor) and the quantitative reasoning and verbal reasoning scores (factor reliability, Bagozzi & Yi, 1988) for quantitative reasoning and verbal reasoning scores is acceptable with 0.70 for quantitative reasoning and 0.75 for verbal reasoning). Hence, quantitative reasoning and verbal reasoning can be interpreted separately. This means, it is possible to measure business and economics quantitative reasoning from scores on a general knowledge test. Thus, Hypothesis A is supported.
We then addressed research question 2: convergent and discriminant validity testing: Hypotheses B to E.3
We focused on the correlation of individual quantitative reasoning scores and mean comparisons with other variables in a nomological network (Section 3). We analyzed whether the pattern of correlations of other variables with quantitative reasoning is what would be expected based on previous research (reviewed above) and whether it supports our hypotheses.
The following variables were used in this correlational analysis:
To test whether these convergent or discriminant external variables supported our expectations they were regressed on the quantitative reasoning and verbal reasoning measures. To this end, model 1 from Section 4 was extended by adding the 5 variables as predictors to the model. Because of the booklet design, this has the advantage that student abilities are not required to be estimated explicitly as, for instance, sum scores, but are estimated within the multiple indicators multiple causes (MIMIC) regression model. This reduces biases because difficulty and discrimination parameters are taken into account. All calculations were again performed with Mplus 7.3 (Muthén & Muthén, 2012). The results of the latent regression model are presented in Table 4.
Table 4
Regression of individual variables on quantitative reasoning (QR) and verbal reasoning (VR) in the chosen business & economics sub-domains (n=1,445)
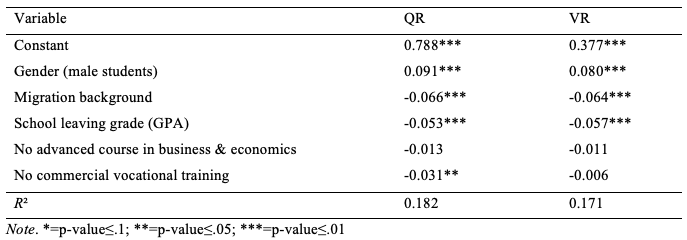
Regarding Hypothesis B that male students perform better than female students, (which is based on all our previous studies in the domain of business and economics, Brückner et al., 2015a), the results meet our expectations for quantitative reasoning but not for verbal reasoning. Thus, Hypothesis B is only partially supported.
Hypothesis C that students with a migration background perform worse than students without a migration background is supported since students with a migration background have lower scores in both quantitative reasoning and verbal reasoning.
Similarly, students with better school leaving grades (with 1 high and 5 low) have a higher score in quantitative reasoning and verbal reasoning and Hypothesis D on the relationship between school leaving grades and test performance in quantitative reasoning items is supported.
In contrast to our expectations regarding Hypothesis E, that prior knowledge in business and economics acquired in advanced courses at vocational schools or in commercial training does not necessarily lead to better performance in tasks that demand quantitative reasoning, we identified a significant impact of the GPA on quantitative reasoning. However, there are no significant effects on the verbal reasoning and no significant effects from attending advanced classes in economics on verbal reasoning and quantitative reasoning.
Moreover, the relationship between quantitative reasoning and vocational training is less strong than the relationship with all other variables, indicating that prior knowledge could be considered a discriminating criterion for quantitative reasoning. Thus, Hypothesis E is only partially supported.
Quantitative reasoning is considered an essential outcome of higher education. While often not directly measured in college, existing tests in business and economics, for example, contain enough quantitative reasoning items to estimate this capacity. This study empirically identifies subsets of items that conceptually measure in business and economics knowledge tests (see research question 1). The analysis confirms that the subset of quantitative reasoning items can be empirically distinguished from verbal reasoning items (as suggested in Hypothesis A). Overall, the internal construct validity of quantitative reasoning was further supported in this study, in line with previous research reported by Brückner et al. (2016).
In terms of convergent and discriminant validity, the analyses indicate that the resulting quantitative reasoning scores correlate, as expected, with the external criteria focused on in this paper (research question 2). More specifically, male students perform better than female students on a business and economics quantitative reasoning subtest (as suggested in Hypothesis B). However, male students also outperform female students on verbal reasoning tasks. Further analyses are therefore necessary to determine the underlying reasons, e.g., whether these differences become manifest due to the quantitative nature of these tasks, or whether it is rather a general domain-specific effect in the tasks that is decisive here.
Students with a migration background have lower scores in a business and economics quantitative reasoning subtest than students without migration backgrounds (as suggested in Hypothesis C). However, this difference became evident in a verbal reasoning subset as well, and will therefore require further investigation in future research.
Furthermore, we have found a relationship between school leaving grades (GPA) and scores in a business and economics quantitative reasoning and verbal reasoning subtests (as suggested in Hypothesis D). This finding is in line with other studies, which show correlations between generic skills like quantitative reasoning and verbal reasoning, and scores in domain-specific tasks.
Finally, our results indicate that students who have pursued advanced courses in business and economics do not perform significantly better than students who have no prior education in business and economics in a quantitative reasoning (or verbal reasoning) subtests (as suggested in Hypothesis E). However, students who have completed commercial vocational training outperform students without vocational training on quantitative reasoning but not verbal reasoning. Although this effect is small, this finding contradicts our assumption. However, numerous studies show similar weak correlations between generic skills like quantitative reasoning and domain-specific knowledge, and such relations are also plausible in context of the development of cognitive outcomes (see Figure 1).
To summarize, the present analyses indicate that it is possible to use a knowledge test in the domain of business and economics and identify a reliable and valid subset of items that conceptually measure quantitative reasoning. In terms of construct validity of quantitative reasoning as an indirect measure out of a domain-specific knowledge test, the findings show evidence to support these resulting scores as a valid measure for quantitative reasoning in business and economics.
While it is possible to get valid a measure of quantitative reasoning with a domain-specific knowledge test if the domain deals with numeric properties or quantitative features in its contents, the number of existing test items was not equally distributed between both quantitative reasoning and verbal reasoning. Furthermore, when it comes to explaining differences between students’ test performances in terms of the two factors quantitative reasoning and verbal reasoning, there might be other, e.g. more general domain-specific or task-related effects in play which were not controlled or discovered here. For instance, in another study on the TUCE, the linguistic properties of the 60 test items used can explain up to 25% of performance without considering any other attributes such as gender or prior knowledge (Mehler et al., 2018). Neither these nor other features of the TUCE tasks, particularly when comparing quantitative reasoning and verbal reasoning tasks, have been investigated so far in the research of quantitative reasoning in a specific domain.
In future studies, therefore, we should examine whether and to what extent quantitative reasoning and verbal reasoning tasks differ in for instance linguistic features. The empirical differentiability and the significance of spatial reasoning (SR) in relation to verbal reasoning and quantitative reasoning should also be researched using suitable test instruments. Here, performance assessments in simulating more complex realistic scenarios show particularly interesting potential (Shavelson et al., 2019).
The correlation between quantitative reasoning and thinking and understanding in business and economics needs to be examined in a much more detailed and differentiated manner. Future studies should assess the role of quantitative reasoning using separate quantitative reasoning tests as external criteria of quantitative reasoning to validate the factor-based quantitative reasoning test scores, their relationship to domain-specific content knowledge (e.g., final grades in a bachelor’s degree program), and their incremental predictive validity. In this context, another important step would be to examine in more detail to what extent these skills are generic or to what extent they also encompass domain-specific components, which is still a fundamental underresearched question.
Despite these limitations, this study supports the crucial role of quantitative reasoning in solving business and economics tasks. In terms of implications for educational practice, this skill needs more curricular and instructional attention in developing (domain-specific) expertise in higher education. Teaching quantitative reasoning should be anchored more deeply in economic education to reduce the substantial deficits in corresponding skills among students as shown in other studies (e.g., Brückner et al., 2016). In this context, an objective, reliable, and valid assessment of students’ quantitative reasoning development provides a necessary basis for various diagnostic and instructional purposes in and outside of higher education. Understanding how students learn and implement quantitative reasoning to solve domain-specific tasks, and how these skills develop throughout their academic studies can help educational practitioners to develop (more) effective tailored instruction to promote the development of quantitative reasoning among students. This may improve students’ learning outcomes and domain-specific performance. The newly developed methodological approach presented in this paper, which is based on gaining information on students’ quantitative reasoning using existing domain-specific tests, offers a practical alternative to broad time- and resource-intensive test batteries for valid measuring students’ learning outcomes in higher education.
We would like to thank the two reviewers who provided constructive feedback and helpful guidance in the revision of this manuscript.
1Although there is extensive research regarding general cognitive abilities and their correlates (Carroll, 1993), this and related work does not take into account domain-specificity in thought processes when it comes to quantitative reasoning.
2ANONYMIZED is the acronym for the title ‘Modeling and Measuring Competencies in Business and Economics among Students and Graduates by Adapting and Further Developing Existing American and Mexican Measuring Instruments (TUCE/ EGEL). For further information, "https://www.blogs.uni-mainz.de/fb03-wiwi-competence-1/"
3To further evaluate the validity of our interpretation of quantitative reasoning test scores, we examined and reported on test content and student response processes in previous studies (following AERA et al., 2014). The validity criterion ‘test content’ was important in adapting TUCE and EGEL items to the German context. Content analyses in the form of curricular analyses, expert interviews, and online ratings (Zlatkin-Troitschanskaia et al., 2014) provide support for the claim that the test also measures skills demanding quantitative reasoning. Evidence from ‘think aloud’ or ‘cognitive interviews’ with students supports ‘response processes’ claims. The findings of the quantitative analyses presented here were also confirmed in think aloud interviews with the test takers (Brückner & Pellegrino, 2016).
Alexander, P. A., & Jetton, T. L. (2003). Learning from traditional and alternative texts: New conceptualization for an information age. In A. C. Graesser, M. A. Gernsbacher & S. R. Goldman (Eds.), Handbook of Discourse Processes (pp. 199–241). Lawrence Erlbaum Associates.
Anderson, J. R. (2005). Cognitive Psychology and its Implications (6th ed.). Worth.
Association of American Colleges and Universities (AAC&U). (2008). College learning for the new global century. https://secure.aacu.org/AACU/PDF/GlobalCentury_ExecSum_3.pdf
Bagozzi, R. P., & Yi, Y. (1988). On the evaluation of structural equation models. Journal of the Academy of Marketing Science, 16 (1), 74–94. https://doi.org/10.1007/BF02723327
Ball, D. L. (2003). Mathematical proficiency for all students: Toward a strategic research and development program in mathematics education. RAND Mathematics Study Panel.
Ballard, C. L., & Johnson, M. F. (2004). Basic math skills and performance in an introductory economics class. The Journal of Economic Education, 35(1), 3–23. https://doi.org/10.3200/JECE.35.1.3-23
Bleske-Rechek, A., & Browne, K. (2014). Trends in GRE scores and graduate enrollments by gender and ethnicity. Intelligence, 46, 25–34. https://doi.org/10.1016/j.intell.2014.05.005
Brückner, S., Förster, M., Zlatkin-Troitschanskaia, O., Happ, R., Walstad, W.B., Yamaoka, M., & Asano, T. (2015a). Gender effects in assessment of economic knowledge and understanding: Differences among undergraduate business and economics students in Germany, Japan, and the United States. Peabody Journal of Education, 90(4), 503–518. https://doi.org/10.1080/0161956X.2015.1068079
Brückner, S., Förster, M., Zlatkin-Troitschanskaia, O., & Walstad, W. B. (2015b). Effects of prior economic education, native language, and gender on economic knowledge of first-year students in higher education. A comparative study between Germany and the USA. Studies in Higher Education, 40(3), 437–453. https://doi.org/10.1080/03075079.2015.1004235
Brückner, S., & Pellegrino, J. W. (2016). Integrating the analysis of mental operations into multilevel models to validate an assessment of higher education students’ competency in business and economics. Journal of Educational Measurement, 53(3), 293–312. https://doi.org/10.1111/jedm.12113
Byrne, M., & Flood, B. (2008). Examining the relationship among background variables and academic performance of first year accounting students at an Irish University. Journal of Accounting Education, 26(4), 202–212. https://doi.org/10.1016/j.jaccedu.2009.02.001
Carroll, J. B. (1993). Human cognitive abilities: A survey of factor-analytic studies. Cambridge University Press. https://doi.org/10.1017/CBO9780511571312
CENEVAL (Centro Nacional de Evaluación para la Educación Superior). (2011). Examen General para el Egreso de la Licenciatura en Administración. EGEL-ADMON . CENEVAL.
Davidson, M., & McKinney, G. G. R. (2001). Quantitative reasoning: An overview. Dialogue, 8, 1–5.
ETS (Educational Testing Service). (2016). GRE: Guide to the use of scores 2016-17. https://www.ets.org/s/gre/pdf/gre_guide.pdf
Elrod, S. (2014). Quantitative Reasoning: The Next "Across the Curriculum" Movement. Peer Review, 16(3), 4–8. https://search.proquest.com/docview/1698319962?accountid=14632
Follette, K., Buxner, S., Dokter, E., McCarthy, D., Vezino B., Brock, L., & Prather, E. (2017). The Quantitative Reasoning for College Science (QuaRCS) Assessment 2: Demographic, Academic and Attitudinal Variables as Predictors of Quantitative Ability. Numeracy, 10(1), 1–33. https://doi.org/10.5038/1936-4660.10.1.5
Förster, M., Brückner, S., & Zlatkin-Troitschanskaia, O. (2015). Assessing the financial knowledge of university students in Germany. Empirical Research in Vocational Education and Training, 7(6), 1–20. https://doi.org/10.1186/s40461-015-0017-5
Frey, A., Hartig, J., & Rupp, A. A. (2009). An NCME Instructional Module on Booklet designs in large-scale assessments of student achievement: Theory and practice. Educational Measurement: Issues and Practice, 28(3), 39–53. https://doi.org/10.1111/j.1745-3992.2009.00154.x
Fritsch, S., Berger, S, Seifried, J., Bouley, F., Wuttke, E., Schnick-Vollmer, K., & Schmitz, B. (2015). The impact of university teacher training on prospective teachers’ CK and PCK – a comparison between Austria and Germany. Empirical Research in Vocational Education and Training, 7(4), 1–20. https://doi.rog/10.1186/s40461-015-0014-8
Gaze, E. C., Montgomery, A., Kilic-Bahi, S., Leoni, D., Misener, L., & Taylor, C. (2014). Towards developing a quantitative literacy/reasoning assessment instrument. Numeracy, 7(2), 4. https://doi.org/10.5038/1936-4660.7.2.4
Happ, R., Zlatkin-Troitschanskaia, O., & Förster, M. (2018). How prior economic education influences beginning university students’ knowledge of economics. Empirical Research in Vocational Education and Training, 10(5), 1–20. https://doi.org/0.1186/s40461-018-0066-7
Hart Research Associates. (2009). Learning and assessment: Trends in undergraduate education. A survey among members of the Association of American Colleges and Universities . http://www.aacu.org/membership/documents/2009MemberSurvey_Part1.pdf
ITC (International Test Commission). (2005). ITC Guidelines for Translating and Adapting Tests. https://www.intestcom.org/files/guideline_test_adaptation.pdf
Kuncel, N. R., Wee, S., Serafin, L., & Hezlett, S. A. (2010). The validity of the Graduate Record Examination for master’s and doctoral programs: A meta-analytic investigation. Educational and Psychological Measurement, 70(2), 340–352. https://doi.org/10.1177/0013164409344508
Lusardi, A., & Wallace, D. (2013). Financial literacy and quantitative reasoning in the high school and college classroom. Numeracy, 6 (2), Article 1. https://doi.org/10.5038/1936-4660.6.2.1
Madison, B. L. (2009). All the more reason for QR across the curriculum. Numeracy, 2(1), Article 1. https://doi.org/10.5038/1936-4660.2.1.1
Mehler, A., Zlatkin-Troitschanskaia, O., Hemati, W., Molerov, D., Lücking, A., & Schmidt, S. (2018). Integrating computational linguistic analysis of multilingual learning data and educational measurement approaches to explore student learning in higher education. In O. Zlatkin-Troitschanskaia, G. Wittum & A. Dengel (Eds.), Positive learning in the age of information (pp. 145–193). Springer VS. https://doi.org/10.1007/978-3-658-19567-0_10
Mislevy, R. J., & Haertel, G. D. (2006). Implications of evidence-centered design for educational testing. Educational Measurement: Issues and Practice, 25(4), 6–20. https://doi.org/10.1111/j.1745-3992.2006.00075.x
Muthén, L. K., & Muthén, B. O. (2012). Mplus user’s guide (7th ed.). Muthén & Muthén.
NRC (National Research Council). (2012). Education for life and work: Developing transferable knowledge and skills in the 21st century. https://nap.nationalacademies.org/catalog/13398/education-for-life-and-work-developing-transferable-knowledge-and-skills
OECD (Organisation for Economic Co-operation and Development). (2013). The Survey of Adult Skills: Reader’s Companion. https://www.oecd.org/skills/piaac/Skills%20(vol%202)-Reader%20companion--v7%20eBook%20(Press%20quality)-29%20oct%200213.pdf
O’Neill, P. B., & Flynn, D. T. (2013). Another curriculum requirement? Quantitative reasoning in economics: Some first steps. American Journal of Business Education, 6(3), 339–346. https://doi.org/10.19030/ajbe.v6i3.7814
Owen, A. L. (2012). Student characteristics, behavior, and performance in economics classes. In G. M. Hoyt & K. M. McGoldrick (Eds.), International Handbook on Teaching and Learning Economics (pp. 341–350). Edward Elgar.
Rocconi, L. M., Lambert, A. D., McCormick, A. C., & Sarraf, S. A. (2013). Making college count: an examination of quantitative reasoning activities in higher education. Numeracy, 6(2), 1–20. https://doi.org/10.5038/1936-4660.6.2.10
Roohr, K. C., Graf, E. A., & Liu, O. L. (2014). Assessing quantitative literacy in higher education: An overview of existing research and assessments with recommendations for next-generation assessment. ETS Research Report Series, 2014(2), 1–26. https://doi.org/10.1002/ets2.12024
Satorra, A., & Bentler, P. M. (2010). Ensuring positiveness of the scaled difference chi-square test statistic. Psychometrika, 75(2), 24–248. https://doi.org/10.1007/s11336-009-9135-y
Schreiber, J. B., Nora, A., Stage, F. C., Barlow, E. A., & King, J. (2006). Reporting structural equation modeling and confirmatory factor analysis results. A review. The Journal of Educational Research, 99(6), 323–338. https://doi.org/10.3200/JOER.99.6.323-338
Schuler, H., Funke, U., & Baron-Boldt, J. (1990). Predictive validity of high-school grades: A meta-analysis. Applied Psychology: An International Review, 39(1), 89–103. https://doi.org/10.1111/j.1464-0597.1990.tb01039.x
Shavelson, R. J. (2008). Reflections on quantitative reasoning: An assessment perspective. In B. L. Madison & L. A. Steen (Eds.), Calculation vs. context. Quantitative literacy and its implications for teacher education (pp. 27–44). Mathematical Association of America.
Shavelson, R. J., & Huang, L. (2003). Responding responsibly to the frenzy to assess learning in higher education. Change. The Magazin of Higher Learning, 35(1), 10–19. https://doi.org/10.1080/00091380309604739
Shavelson, R. J., Marino, J. P., Zlatkin-Troitschanskaia, O., & Schmidt, S. (2019). Reflections on the assessment of quantitative reasoning. In B. L. Madison & L. A. Steen (Eds.), Calculation vs. context: Quantitative literacy and its implications for teacher education . Mathematical Association of America.
Tiffin, P. A., McLachlan, J. C., Webster, L., & Nicholson, S. (2014). Comparison of the sensitivity of the UKCAT and A levels to sociodemographic characteristics: A national study. BMC Medical Education, 14(7), 1–12. https://doi.org/10.1186/1472-6920-14-7
Williams, M. L., Waldauer, C., & Duggal, V.G. (1992). Gender differences in economic knowledge: An extension of the analysis. The Journal of Economic Education, 23(3), 219–231. https://doi.org/10.1080/00220485.1992.10844756
Yamaoka, M., Walstad, W. B., Watts, M. W., Asana, T., & Abe, S. (Eds.). (2010). Comparative studies on economic education in Asia-Pacific region. Shumpusha.
Zahner, D. (2013). Reliability and validity of CLA +. Council for Aid to Education.
Zlatkin-Troitschanskaia, O., Förster, M., Brückner, S., & Happ, R. (2014). Insights from a German assessment of business and economics competence. In H. Coates (Ed.), Higher education learning outcomes assessment (pp. 175–200). Peter Lang.
Zlatkin-Troitschanskaia, O., Förster, M., Schmidt, S., Brückner, S., & Beck, K. (2015). Erwerb wirtschaftswissenschaftlicher Fachkompetenz im Studium. Eine mehrebenenanalytische Betrachtung von hochschulischen und individuellen Einflussfaktoren [Acquisition of economic competence over the course of studies. A multilevel consideration of academic and individual determinants]. In S. Blömeke & O. Zlatkin-Troitschanskaia (Eds.), Kompetenzen von Studierenden (pp. 116–134). Beltz Juventa. https://doi.org/10.25656/01:15506
Zlatkin-Troitschanskaia, O., Shavelson, R. J., & Pant, H. A. (2017). Assessment of learning outcomes in higher education – international comparisons and perspectives. In C. Secolsky & B. Denison (Eds.), Handbook on measurement, assessment and evaluation in higher education (2nd ed.). Routledge.